Logarithm with the Examples [Page 1]

Now I want to let you know about Logarithm, I also provide the example of it so you can understand how their works..

What is an Exponent?

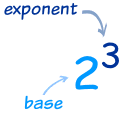The exponent of a number says how many timesto use the number in a multiplication. In this example: 23 = 2 × 2 × 2 = 8 (2 is used 3 times in a multiplication to get 8)

What is a Logarithm?

A Logarithm goes the other way.

It asks the question "what exponent produced this?":

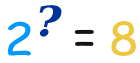
And answers it like this:

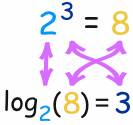
In that example:

• The Exponent takes 2 and 3 and gives 8 (2, used 3 times, multiplies to 8)
• The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication)

A Logarithm says how many of one number to multiply to get another number

So a logarithm actually gives you the exponent as its answer:

(Also see how Exponents, Roots and Logarithms are related.)

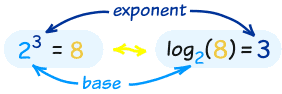
Working Together

Exponents and Logarithms work well together because they "undo" each other (so long as the base "a" is the same):

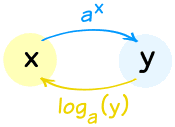
They are "Inverse Functions"

Doing one, then the other, gets you back to where you started:

• Doing a^x, and then the logarithm, gives you x back again:
• Doing the logarithm, then a^x , gives you x back again: 

It is too bad they are written so differently ... it makes things look strange.

So it may help you to think of a^x as "up" and log_a(x) as "down":

• going up, then down, returns you back again: down(up(x)) = x , and
• going down, then up, returns you back again: up(down(x)) = x

Anyway, the important thing is that:

The Logarithmic Function can be "undone" by the Exponential Function.

(and vice versa)

Like in this example:

Example, what is x in log₃(x) = 5

We can use an exponent (with a base of 3) to "undo" the logarithm:

Start with
We want to "undo" the log so we can get "x ="
Use the Exponential Function (on both sides!):
And we know that , so:		x = 35
Answer:		x = 243

And also:

Example: Calculate y in y= log₄ (1/4)

Start with
Use the Exponential Function on both sides:
Simplify:		4y = 1/4
Now a simple trick: 1/4 = 4-1
So:		4y = 4-1
And so:		y = -1