Introduction
Indices are a useful way of more simply expressing large numbers. They also present us with many useful properties for manipulating them using what are called the Law of Indices.
What are Indices?
The expression 25 is defined as follows:
We call "2" the base and "5" the index.
Law of Indices
To manipulate expressions, we can consider using the Law of Indices. These laws only apply to expressions with the same base, for example, 34 and 32 can be manipulated using the Law of Indices, but we cannot use the Law of Indices to manipulate the expressions 35 and 57 as their base differs (their bases are 3 and 5, respectively).
There have SIX rules of the Law of Indices
Rule 1: 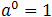
Any number, except 0, whose index is 0 is always equal to 1, regardless of the value of the base.
An Example:
Simplify 20:
| Rule 2: | |
An Example:
Simplify 2-2:

Rule 3: 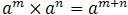
To multiply expressions with the same base, copy the base and add the indices.
An Example:
Simplify 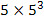 : (note: 5 = 51)
: (note: 5 = 51)

Rule 4: 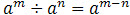
To divide expressions with the same base, copy the base and subtract the indices.
An Example:
| Simplify | |

Rule 5: 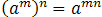
To raise an expression to the nth index, copy the base and multiply the indices.
An Example:
Simplify (y2)6:

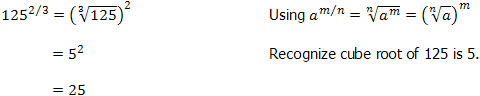
| Rule 6: | |
An Example:
Simplify 1252/3:
No comments:
Post a Comment